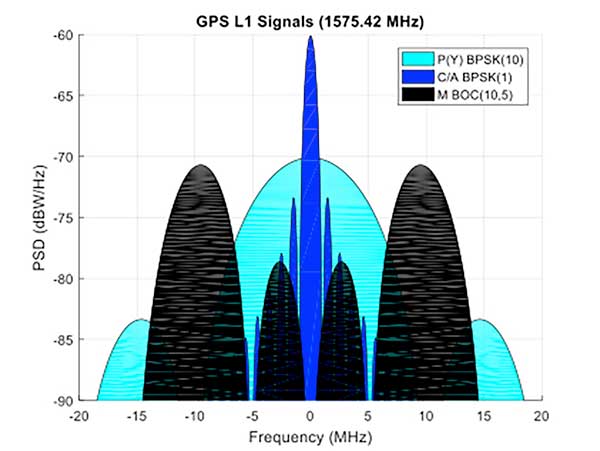
Teooria.
GNSS (GPS) juhitavat moona on põhimõtteliselt kahte erinavat sorti:
Spin-stabilized (nt. XM 1156)
Fin-stabilized (nt. M712 Copperhead ; M982 Excalibur)
Spin-stabilized moona iseärasuste kohta saab lugeda siit:
https://www.hindawi.com/journals/ijae/2015/908304/
Ukraina kontekstis tekkis probleem väidetavalt M982 Excalibur moonaga.
Juhitav moon vajab sihtmärgile jõudmise programmeerimiseks laskmiskohas:
* laskeseadme täpset asukohta (X;Y;Z koordinaate)
* sihtmärgi täpset asukohta (X;Y;Z koordinaate)
[algandmed, mis sisestatakse juhitavasse moona, et see saaks teha vastavaid arvutusi lennu ajal]
* algset välja arvutatud
direktsiooninurka ja relva/laskeseadme suunamist selles suunas
* võimalik, et ilmastiku jms muutuvaid parameetreid (nt. tuulesuund ning tugevus).
* GPS MIL koodide (ja krüpteeritud P/Y ja M juurdepääsuparoolide/võtmete?) sisestamist
* veel midagi?
Teoreetiliselt (mina ei tea nüansse peensusteni) peaks tarkmoon juba laskeseadmes hakkama suhtlema sattidega (initsialiseerimine ja selleks kuluv aeg/vajaliku hulga sattide leidmine). Hiljemalt lasu/stardi hetkest alates ta igatahes seda tegema hakkab.
EXAMPLE 100 ms PIK TO PROJECTILE MESSAGE FRAME
• Sense when Time Mark Pulse (TMP) arrives
• Read Time Mark Message from GPS receiver
• Send Time Mark Message to Projectile
• Send Target and Gun data to Projectile
• Request a Status Message from Projectile
• Receive and Process the Projectile Status
https://ndiastorage.blob.core.usgovclou ... walker.pdf
Edasi on kolm erinevat põhimõtet targa moona sihtmärgile juhtimiseks. Neid võib kasutada nii üksikult kui omavahel kombineeritult.
Kolm peamist juhiste tüüpi, mida juhitava laskemoona kontekstis kõige sagedamini kasutatakse, on trajektoori kujundamine, trajektoori ennustamine ja trajektoori jälgimine.
4.1 Ennustav juhendamine
Ennustavas juhises (PG) kasutatakse igas juhiste värskendamise hetkes mürsu ja keskkonna mudelit, et arvutada välja juhtimistoimingute jada, mis annaks praeguse oleku korral sihtmärgini viiva lennutrajektoori. Kui mudelis ja mõõtmistes pole vigu (ja kõik olekud on mõõdetavad), piisab sellest ühest juhise arvutamise hetkest ja sellest tulenevast juhtimistoimingust, et anda lennutrajektoori, mis viib mürsu kuni sihtmärgini. Kuid tegelikkuses on lennu ajal vaja teha vähemalt paar sellist arvutust koos kaasneva trajektoori parandusega.
Ma ei hakka kogu juttu siia uuesti panema.
Põhimõtteliselt sisestatakse esmased andmed (ja tehakse initsialiseerimine?) ja siis kui moon stardib, tehakse kohe GPS initsialiseerimine kui enne pole tehtud, kogutakse muud algandmed (lennukiirus, pöörlemiskiirus, tõusunurk jne) ning tehakse vajalikud arvutused, et moon viia õigele lennutrajektoorile. Kui algandmed on valed (nt. lähtepunkti GPS koordinaadid X;Y;Z, valesti määratud põhjasuund ja direktsiooninurk, vale kiirus, vale kõrgus jne) siis arvutatakse moonale vale suund ja trajektoor. Mida kaugemal on sihtmärk seda rohkem lendab sellisel juhul moon sellest mööda + seda suurem tekib kas puudulend või ülelend.
Nüüd edasi oleneb juhtimispõhimõttest ja moona lennu suunakorrigeerimise edaspidisest vajadusest ning võimekusest.
Lisaks tuleb arvestada, et Excaliburil on ka mingi INS (inertsiaalnavi) võimekus mida saab kasutada ilma GPS toeta kui selle signaal kaob.
Osa andmeid arvutusteks tulevad pidevalt jooksvalt INS plokist ja need tulevad ka siis kui GPS signaali ei ole.
Edasi on kolm põhilist lennufaasi. Stardijärgne kiirenduse ja tippkiiruse saavutamise faas, tipufaas ja terminalifaas/lõppfaas.
Ülehelikiiruse faas on trajektoori osa, kus mürsk on relvale kõige lähemal ja kus on kõige lihtsam andmeid üles linkida. Üleslingi andmed võivad hõlmata mürsu tegeliku algkiiruse mõõtmisi ja mürsu asukoha ja kiiruse radarimõõtmisi. See on ka osa, kus iga inertsiaalset navigatsioonisüsteemi (INS) saab ja tuleks lähtestada ning kus GPS saab hakata satelliidiandmeid hankima.
Terminali faas on lennutrajektoori viimane kolmandik.... just selles faasis on GPS signaali segamise/summutamise tõenäosus suurim, kui navigeerimiseks kasutatakse GPS-i.
Rõhk sõnal TÕENÄOSUS ehk, et eeldatakse, et stardiseadme juures on kõik õige ja vastane pääseb moona GPS andmeid mõjutama tõenäoliselt alles lennu lõppfassis, kuna EW vahendid on pandud sihtmärgi kaitseks.
Seega on GPS ja INS juhitav tarkmoon GPS jammimisele kõige haavatavam (jammimine avaldab lõpptulemusele kõige suuremat mõju) lennu algfaasis ja lennu lõppfassis. Kui jammimine/segamine toimub lennu keskmises faasis siis
a) algandmed on jätkuvalt õiged, välja on arvutatud õige direktsiooninurk, suund, teekond, trajektoor
b) keskmises faasis kadunud side GPS andmetega ei võimalda teha ülitäpseid asukohaparandusi (kui neid on vaja teha) lennu keskel, kuid moon liigub endiselt õiges suunas ja abiks on ka INS
c) lõppfaasis taastunud GPS andmeside võimaldab teha vajalikud täpisparandused ja korrigeerimised ning need jõutakse ka ellu viia, sest moon on liikunud kõigele vaatamata jämedalt võttes õiges suunas ja vajalik korrigeerimise suurus ei ole liiga suur ega ülejõu käiv.
Kui jammimine/segamine on algfaasis, siis on kõik arvutused valed, moon on viidud valele trajektoorile, valele kõrgusele, valele teekonnale, lendab vales suunas ja tekib lisaks kas puudulend või ülelend. Kui valedest algandmetest põhjustatud vead ei ole liiga suured ja hiljem mingis faasis taastub GPS side ning on võimalik moona asukohta täpselt määrata, tehakse uued arvutused ja siis suudab moon enda lendu vbl piisavalt hiljem korrigeerida, et ikkagi õigesse lõpp-punkti jõuda. Oleneb ka algtrajektoorist ja palju see erineb "tõelisest/õigest". Kui algvead on liiga suured ei suuda moon enam ennast õigele trajektoorile viia.
Kui jammimine on lõppfassis, siis algandmed on jätkuvalt õiged, välja on arvutatud õige direktsiooninurk, suund, teekond, trajektoor. Lennu keskmises faasis on saadud vajalikud täiendavad parandid lennu "peenhäälestamiseks" ja kui lõppfaasis kaobki GPS andmeside, siis INS hoiab kurssi mis oli arvutatud viimasel hetkel kui GPS andmed veel saadavad olid.
Seega teoreetiliselt on kõige hullemast variandist kõige parema variandini jammimise/signaalisegamise mõju järgmine:
* Jammitud on kõik kolm lennufaasi
* jammitud on esimene ja viimane lennufaas
* jammitud on esimene ja keskmine lennufaas
* jammitud on esimene lennufaas
* jammitud on keskmine ja viimane lennufaas
* jammitud on viimane lennufaas
* jammitud on keskmine lennufaas
* jammitud pole ükski lennufaas
Edasi vaatame olukorda vastase poolt.
Sul on 20 kriitilist objekti kuhu võib lennata tark täpismoon.
Nende kaitsmiseks oleks vaja 20 EW jaama, eraldi iga objekti lähedal, et jammida moona viimast lennufaasi ja loota, et see mõjutab piisavalt.
Kui sa paned oma ühe EW jaama "õigesse kohta" millega suudad ära jammida vastase laske/stardiseadme enda ja esimese (ja vbl ka keskmise) lennufaasi), siis kõik 20-ne objekti pihta lastud moon sellest stardiplatvormist lendab tõenäoliselt mööda. Siin oleneb jälle moonast, kas on spin-stabilized või end-stabilized jne sest neil on erinevad juhtimismeetodid ja trajektoorid ja haavatavused GPS signaali puudumisele jne.
Eelnev teooria puudutab "jammimist" ehk GPS signaali segamist/summutamist.
Kui aga on tegemist
GPS spoofinguga, siis on juba hoopis teised jutud.
*
A simulation of a GPS-INS guided artillery shell was used to analyze the sensitivity of miss distance to unmodeled errors in aerodynamic and environmental parameters. Based on the sensitivity analysis, a Kalman filter was designed to estimate errors in coefficient of drag, coefficient of pitching moment, initial velocity and the horizontal wind component.
These unmodeled errors, which are countered by active guidance in the presence of a GPS signal, could be ameliorated earlier in the flight if they were known, thereby reducing the impact of GPS-jamming in the final portions of flight.
1.3 GPS Jamming and the GPS/MMIMU
A typical terrestrial GPS user with a small, fixed antenna, sees less than 10- 15 W of signal power from each space vehicle. Such a low signal power at the receiver makes hostile jamming a serious concern. In fact, jammers that are man-portable and require less than 10 W are currently available on the world arms market. The possibility of widespread jamming of the GPS signal over target areas poses a potential operational problem for the SSHP in light of the relatively poor error stability of the SSHP micromechanical inertial instruments. The end effect of the relatively unstable inertial instrument errors is the loss of useful navigation data a matter of tens of seconds after the loss of GPS updates. Projected improvements in micromechanical inertial instrument performance will significantly improve this aspect of navigation performance. GPS updates are used to estimate and contain the inertial instrument errors and in the absence of these updates, the navigation solution rapidly loses practical value.
Given the necessity of GPS updates to SSHP navigation and guidance, anti-jam performance is an important consideration in the SSHP concept. Two of the possible anti-jam modifications use a segmented GPS antenna to partially isolate and identify noise. Obviously, once the local vertical has been determined and GPS has been reacquired, the antenna patches facing the sky-- and hence the GPS space vehicles--can be relied upon to have a small component of ground-noise and ground-based jamming signal. Using only those antenna patches that are facing the sky will, however, reduce the number of available space vehicles by masking those satellites that are low on the horizon and to the side of the shell. This not only has the effect of decreasing the accuracy of the GPS measurement but could possibly reduce the number of available satellites below the minimum of four. Alternatively, the design could be augmented to include a home-on-jam capability that uses the ground-facing antenna patches to identify and guide the round toward ground based jamming sites. While this may be desirable from an operational point of view, home-on-jam does not improve the accuracy of the SSHP with respect to the original target. A third anti-jam strategy would be to estimate parameters that alter the ballistic trajectory and correct the stored trajectory accordingly.
Since the guidance algorithm has no capability to determine the magnitude of these unmodeled errors and hence has no capability to correct the offset targets for them, a SSHP round in the presence of GPS jamming and modeling or environmental errors would, in effect, be an unguided artillery shell on a trajectory that does not intersect the target. That is, the trajectory used to produce the offset targets is not the path that a round would follow in the presence of aerodynamic, environmental or initial condition dispersions.
One solution to this potential problem is to estimate these errors while the navigator is receiving GPS updates and correct the intended ballistic path accordingly. An optimal--in the minimum variance sense--estimation algorithm, known as a Kalman filter, is employed to determine the value of these errors. Generally, this algorithm measures the position and velocity differences between the ballistic trajectory and the actual state of the round and calculates the combination of launch, modeling and environmental errors that are most likely to have produced the measured differences.....
https://dspace.mit.edu/bitstream/handle ... 80-MIT.pdf
between Friday and Sunday this weekend. Earth has only been hit with 3 previous severe CMEs in last 4 years. But we are gonna get 5x G4 CMEs in 3 days!
too!
positioned 1 million miles ahead of each on the Earth-Sun path).
field - if the magnetic shock is same positive as North Pole, it won’t do much. But if opposite field, we will see effects”.
Hence hard to predict effects.
NOAA scientist spokesperson: “Hard to know. Our models say between 2-12%”
between Friday and Sunday this weekend. Earth has only been hit with 3 previous severe CMEs in last 4 years. But we are gonna get 5x G4 CMEs in 3 days!
too!
positioned 1 million miles ahead of each on the Earth-Sun path).
field - if the magnetic shock is same positive as North Pole, it won’t do much. But if opposite field, we will see effects”. 
Hence hard to predict effects.
NOAA scientist spokesperson: “Hard to know. Our models say between 2-12%” 